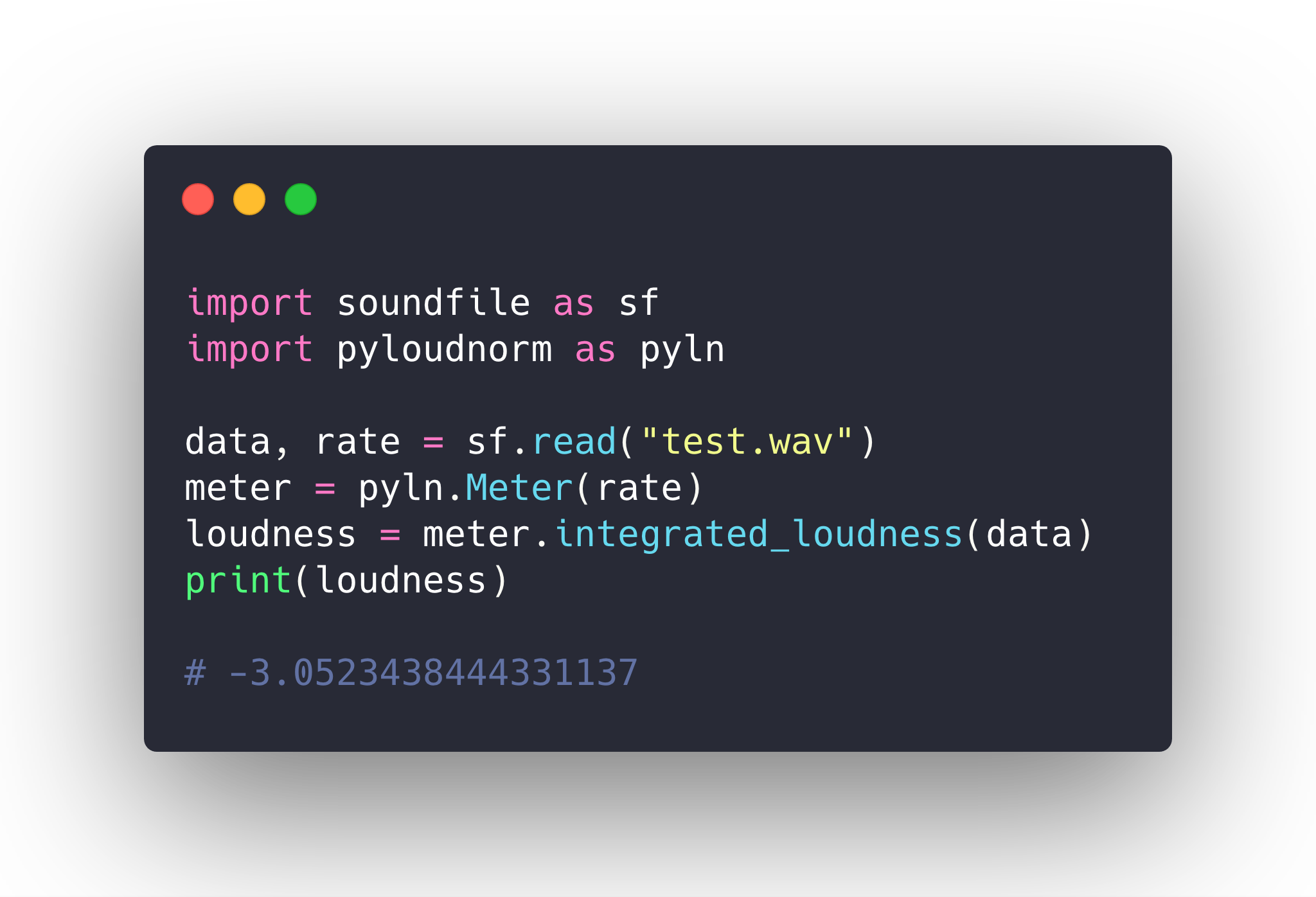
Humans perceive the loudness of sound pressure waves in a subjective, non-linear manner. This makes measuring the perceived loudness of recorded material more difficult than a simple examination of the energy in a signal. The ITU-R BS.1770 standard defines an algorithm for measuring the relative loudness of recorded material within the context of broadcast and cinema. This algorithm now has been applied to many other areas, for example loudness normalization of music in online streaming services, and therefore has become of interest to many. While many real-time and offline implementations exist, a a pure Python framework that allows the user to the adjust parameters of the algorithm (such as pre-filters, gating block size, and channel gains) has not previously existed. pyloudnorm aims to provide this level of control in a Python implementation and depends only on NumPy and SciPy.
pyloudnorm is an open source project. Check it out on GitHub.
For more details read our preprint.
A few commercially available common real-time loudness meter plugins.
Algorithm
You can read through the full algorithm specification in the ITU-R BS.1770-4 standard, but I will give a brief overview here. The block diagram above shows the main four stages of the algorithm for a 5.1 channel signal.
The first stage of the algorithm is comprised of the application of the “K” frequency weighting which is comprised of two IIR filters, a high shelving filter and a high pass filter. There has been much confusion over the proper way to implement these filters since the specification only provides filter coefficients for 48 kHz implementations. This has led to some inconsistency among different implementations since nearly all implementations support operation at different sampling rates and therefore defined their own method of deriving coefficients for alternate sampling rates. Brecht De Man recently published a paper where he went through the arithmetic of deriving the proper filter definitions from the supplied coefficients. He also provided a Python implementation using this method. I am planning to include this coefficient calculation method in pyloudnorm shortly.
The next stage involves computing the mean square value for each channel in the signal and then each channel is weighted where surround channels have larger weights and the LFE channel is ignored. The weighted signals are then summed. A gating process is then applied to this sum which attempts to mitigate the effect of portions of silence or near silence in the signal that would otherwise lower the measured integrated loudness of a signal. Two thresholds are used in this gating process, where the signal is split up into 400 ms blocks with 75% overlap. Each block is then measured against the first threshold at -70 LKFS and the second at -10dB relative to the loudness of the signal once blocks below the -70 LKFS have been removed. Finally the loudness measurement is based upon all gating blocks which contain a measurement above both the absolute and relative thresholds.
Extensibility
At the end of the algorithm specification the authors write:
It should be noted that while this algorithm has been shown to be effective for use on audio programmes that are typical of broadcast content, the algorithm is not, in general, suitable for use to estimate the subjective loudness of pure tones.
This has be observed by many when attempting to measure the perceptual loudness of signals which are not broadband. A number of researchers have investigated possible adjustments to the algorithm that result in more perceptually accurate measurement for narrow band signals. Work by Pestana et. al. made a proposal for modifying the filters and gating method in order to provide more perceptually accurate measurements. Fenton and Lee expanded on this work and produced a series of modifications to algorithm that includes alternate filtering and gating techniques as well. And Fenton recently followed up this work with a new publication that defines alternative filtering and gating techniques tailored to common instrument stems in a multitrack mix with the goal of using this algorithm to perform automatic mixing.
Due to the value of these alternative filtering and gating techniques, it is necessary to provide users with the ability to easily apply these modifications to the core algorithm specification. For that reason pyloudnorm has been built to allow easy programatic control of these settings. Users can choose from filter weighting filters proposed in the literature and even provide their own IIR filter specifications if desired. In addition gating block sizes can easily be adjusted to match recommendations from the literature and also extended. Extensibility of the core ITU-R BS.1770-4 algorithm is the focus of pyloudnorm and enables its use in systems that intent to measure the loudness of narrow band stimuli, notably in the are of automatic mixing, which is what originally motivated this implementation.
In progress
There are still a number of improvements and extensions to be included. The current code is a working base for the project and will continue to be expanded. Some of the future features and functionality are listed below.
Option for compliant filter coefficients based on work by Brecht De Man [ done ]
Momentary and short term loudness measurements
Full code test coverage including tests with the compliance material [ done ]
Adjustable channel weighting and ordering
Contributing
pyloudnorm is an open source project and I welcome any help in improving the project. Please feel free to leave an issue on the GitHub repository if you run into any problems or have suggestions for new features and improvements. Also, if you are interested in contributing I am more than happy to accept pull requests.